丹布朗(Dan Brown)的暢銷小說”達文西密碼”中,出現的第一個數字密碼 13-3-2-21-1-1-8-5 ,牽引出後續的許多懸疑情節,這個數字密碼其實就是鼎鼎大名的費波那西數列的不同排列罷了。而費波那西數列跟我們這裡所要談的數— e 有著非常密切的關係。
在所有的數中,除了0,1和 以外,大概只有e這個數能吸引大多數數學家的眼光了。這個e到底為何數呢?它和計算複利有關,和向日葵花的排列方式有關,和懸著的鏈子有關,和樹木分枝的型態有關,也和雙曲線 底![]() 下的面積有關,這許多看似無關的事物,竟然都和同一個數有關,這就透露著有某種玄機在裏面了,現在讓我們來進行這個探索之旅吧!
下的面積有關,這許多看似無關的事物,竟然都和同一個數有關,這就透露著有某種玄機在裏面了,現在讓我們來進行這個探索之旅吧!
1. 複利計算
人類的歷史中,從發明了錢以後,整個人類的活動就變得頻繁起來了,有了錢,自然也產生了借貸和償還的問題。有借有還,再借不難,但借錢給人家的人總要能從中獲取一些好處吧!也因此就有了利息的計算問題。利息分為單利和複利:單利是每次計息均以本金為基準來產生利息;複利則是每次計息均將上一次產生的利息併入本金當作新的本金來計息。
例如把100元(本金)存進銀行中某個帳戶,若以年利率5%單利計息,則第一年後結存為 100×1.05=105=(100+5)元,利息為5元,第二年結存為100×1.05+5=(100+2×5)元,以此類推第t年後結存為(100+5t) 元。若同樣本金為100元,年利率5%以複利計息,則第一年結存為100×1.05=100×(1+0.05) 元,第二年結存為[100×(1+0.05)]×(1+0.05)=100×(1+0.05)² 元,因此第t年的結存為![]() 元。
元。
現在以一般情況來看,假設將本金P元存入銀行某個帳戶,每年以年利率r(r以小數表示)計息一次,則第一年結存為P(1+r),第二年結存為P(1+r)² ,以此類推第t年結存為![]() ,若以S(t)表示t年後之結存,則S(t)=
,若以S(t)表示t年後之結存,則S(t)= ![]() 。有時候一年不只複利計息一次,譬如以年利率r每半年複利計息一次,則一年計息兩次,但利率也變為
。有時候一年不只複利計息一次,譬如以年利率r每半年複利計息一次,則一年計息兩次,但利率也變為![]() ,t年後之結存
,t年後之結存![]() ,如此可推得本金P,以年利率r,每年複利計息n次,在t年後之結存以A(t)表示,將變為
,如此可推得本金P,以年利率r,每年複利計息n次,在t年後之結存以A(t)表示,將變為![]() ,由此可見每年計息的次數愈多,則所生的利息當然更好,而且似乎如果每天計息,所產生的利息應比每年計息一次所產生的利息多很多。其實不然,自表1中可看出以100元為本金每天計息,只比整年計息一次多0.13元的利息而已,甚至於只比每月計息或每週計息多約0.01元而已,幾乎沒什麼差別。為什麼會如此呢?
,由此可見每年計息的次數愈多,則所生的利息當然更好,而且似乎如果每天計息,所產生的利息應比每年計息一次所產生的利息多很多。其實不然,自表1中可看出以100元為本金每天計息,只比整年計息一次多0.13元的利息而已,甚至於只比每月計息或每週計息多約0.01元而已,幾乎沒什麼差別。為什麼會如此呢?
| 計息週期 | n | r/n | A(1) |
| 每年 | 1 | 0.05 | 105.00元 |
| 每半年 | 2 | 0.025 | 105.06元 |
| 每月 | 12 | 0.004166 | 105.12元 |
| 每週 | 52 | 0.0009615 | 105.12元 |
| 每天 | 365 | 0.0001370 | 105.13元 |
表1. 本金100元,以年息5%,在不同計息週期下一年後之結存狀況
如果更進一步,想像無時無刻都在複利計息,或換句話說,連續的複利計息,亦即計息的期數n趨近於無窮大時,結存會變成 ![]() ,如以m=
,如以m=![]() 代入上式,則
代入上式,則![]() 。
。
在這裏,我們可針對 的值作個探討。在表2中,我們發覺,當m愈來愈大時,![]() 的值似乎增加得愈來愈少,像是會收斂至2.71828附近的數。
的值似乎增加得愈來愈少,像是會收斂至2.71828附近的數。
| m | |
| 1 | 2 |
| 2 | 2.25 |
| 3 | 2.37037 |
| 4 | 2.44141 |
| 5 | 2.48832 |
| 10 | 2.59374 |
| 50 | 2.69159 |
| 100 | 2.70481 |
| 1,000 | 2.71692 |
| 10,000 | 2.71815 |
| 100,000 | 2.71827 |
| 1,000,000 | 2.71828 |
| 10,000,000 | 2.71828 |
![]()
事實上,根據數學家的研究,![]() 為一無限不循環小數,它的值約等於2.718281828459045235360287471352這個數,數學家後來就以英文字母e來代表它,即e =
為一無限不循環小數,它的值約等於2.718281828459045235360287471352這個數,數學家後來就以英文字母e來代表它,即e = ![]() ,而且也陸續發現自然界的許多現象都和這個數有關,並且有許多不同的表示方式,如以無窮級數來表示則為
,而且也陸續發現自然界的許多現象都和這個數有關,並且有許多不同的表示方式,如以無窮級數來表示則為![]() ,也可以用連分數表示為 。
,也可以用連分數表示為 。
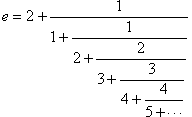
No Comments Yet