在所有的矩形當中，以長寬比等於 的矩形，看起來最順眼，稱為「黃金矩形」，由黃金矩形可產生「黃金螺線」，以此螺線作為圖案的設計基礎，可展現出裝飾設計的多樣變化。如何由黃金矩形來畫出黃金螺線呢?首先由一個黃金矩形開始，以其寬作為一正方形的邊長，將黃金矩形分為一個正方形及一個矩形，此矩形也是黃金矩形，將此新畫出的黃金矩形以同樣的方式再劃分為一個正方形和一個更小的黃金矩形，如此循環下去，可以得到一個黃金矩形的無窮數列;若從最內圈的正方形開始，以正方形的邊長畫四分之一的圓弧，逐步往外延伸，則這些黃金矩形會外切於一條螺線，此螺線稱為「黃金螺線」，如圖9所示。

                         

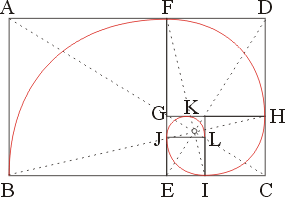
圖9.由黃金矩形畫出黃金螺線的過程

另外一種螺線的畫法可從相鄰兩個正方形所形成的矩形開始，以此矩形之長作為正方形的邊長畫一正方形，此正方形和原先之兩小正方形形成一個矩形，再以此矩形的長為邊長畫一正方形，此正方形和前一個矩形又合成一個更大的矩形，以如此步驟不斷作下去，可作出一系列的正方形，而這些正方形的邊形依序為1,1,2,3,5,8,…正好是費波納西數列，從最小的正方形邊長為半徑畫四分之一弧，同樣的作法一直延伸到後續之每一個正方形，則也會形成一螺線。

黃金螺線為對數螺線的一例，對數螺線最典型的例子為鸚鵡螺的殼(圖10)。那麼對數螺線和e有什麼關係呢？由對數螺線的極座標方程式，，來看就一目了然了。如果再以費波納西數列中相鄰兩數之後項比前項的值約等於黃金數的關係來看，更可見e和費波納西數列、黃金數以及對數螺線彼此之間皆有極密切的關係。

                                    

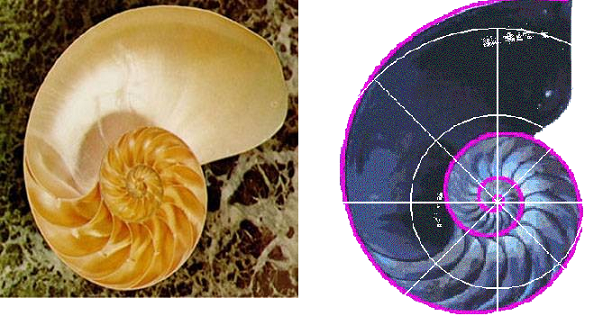
圖10. 鸚鵡螺的殻

在對數螺線的極座標方程式中， ，a是決定螺線增長速率的常數，當a的值為正時，如以逆時鐘方向轉時(即θ角為正)，距極點的距離會愈來愈大(即r的值會遞增)，就會形成一個左旋螺線；當a的值為負時，以逆時鐘方向轉時(即θ角為正)，距極點的距離會愈來愈小(即r的值會遞減)，就會形成一個右旋螺線，圖10中之鸚鵡螺的殻所展示的即為一個右旋螺線。

對數螺線有一最令人驚奇的特性，就是每一條通過極點(中心點)的直線，都會和螺線構成完全相等的交角，也因此稱為等角螺線；簡單的說，也就是它從任何一個方向來看都是一樣的，這個特性使得對數螺線具有像圓一樣的完美對稱性，其實當a的值為0時，可得到 ，正好是半徑為1之圓的極座標方程式，所以對數螺線可算是圓的近親了。此特性的來由主要來自函數 的導數等於它自己這個事實。

對數螺線的另一特性是，當我們把螺線等量旋轉(即讓θ角等量增加)時，距極點的距離r會如等比數列一樣的增加，我們可以從 看出，當增加的角度為固定的ø 值時，r的值可視為一個公比為 的等比數列；從另一層意義來說，任意兩條通過極點的直線，只要夾角一樣，則所切割出來的螺線扇形都是相似的(雖然不全等) 。你是否從圖4中之鸚鵡螺的殻看出其一格一格的腔室形狀皆一樣，而大小卻依等比數列增大？事實上，鸚鵡螺的生長模式為：螺殼每生長出一固定角度，殼內的鸚鵡螺身體就生長出一固定比例，因此，從螺旋形貝殼的形狀，我們可以清楚的看出殼內動物生長的速率.。蘇格蘭動物學家湯普生(D’Arcy W. Thompson, 1860-1948)在他的經典著作《論生長與形態》(On Grown and Form) 中，有非常詳細的討論並指出，許多自然界的動植物之生長形態都偏好對數螺線，例如貝殼、角、長牙、向日葵等。其實這樣的現象並不是偶然的，近代的許多數學家已經研究出其數學模式的成因，例如數學家伏格(H. Vogel)在1979年研究出，向日葵的花之所以形成兩組順時鐘及逆時鐘的螺線，在於其係以最有效率之幾何堆排方式，來使花頭生長得最密實、最堅固。